AA + BB + CC = ABC
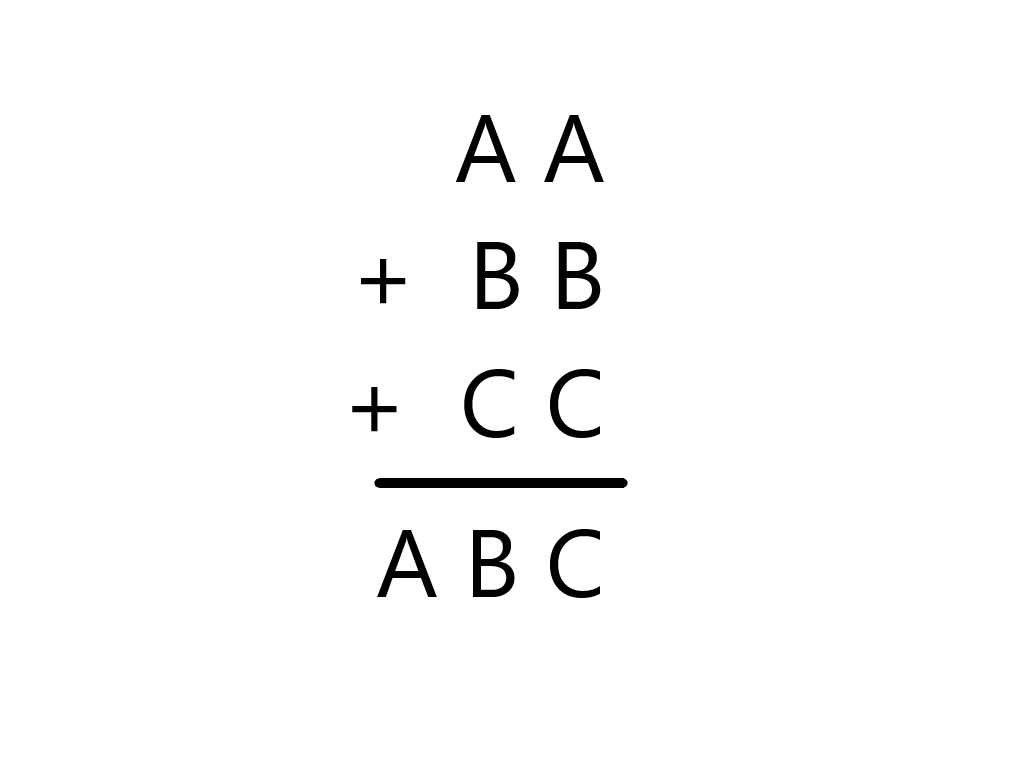
AA + BB + CC = ABC
Find the value of A, B, C.
It is know that value of A, B, and C are single digit and unique.
Answer A = 1, B = 9, c = 8
1 1
+ 9 9
+ 8 8
--------
1 9 8
Explanation:
All A, B and C are unique
Addition of any three unique number's carry is 1 or 2
Therefore the value of A can be 1 or 2
Case 1: A = 2 & B = 9
AA + BB = 22 + 99 = 121
Therefore 121 + CC = 29C
2 + C = 9
so C = 7
22 + 99 + 77 is not equals to 297
Therefore Case 1 failed
Case 2: A = 1 & B = 9
11 + CC = 110
110 + CC = 19C
1 + C = 9
C = 8
Find the value of A, B, C.
It is know that value of A, B, and C are single digit and unique.
Answer A = 1, B = 9, c = 8
1 1
+ 9 9
+ 8 8
--------
1 9 8
Explanation:
All A, B and C are unique
Addition of any three unique number's carry is 1 or 2
Therefore the value of A can be 1 or 2
Case 1: A = 2 & B = 9
AA + BB = 22 + 99 = 121
Therefore 121 + CC = 29C
2 + C = 9
so C = 7
22 + 99 + 77 is not equals to 297
Therefore Case 1 failed
Case 2: A = 1 & B = 9
11 + CC = 110
110 + CC = 19C
1 + C = 9
C = 8

